PI

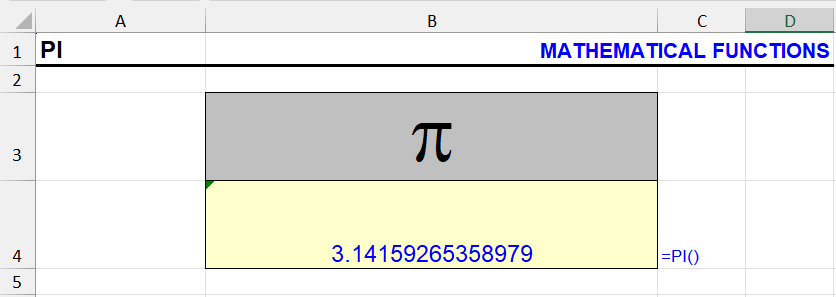
This function returns the value of Pi with an accuracy of 14 decimal places. The function doesn’t require any arguments, it returns the value by itself. Similar functions without arguments – RAND, TODAY, NOW.

Pi is an irrational number, and there are no simple ways to calculate it, which is why such a function exists.

Syntax

=PI()

Formula examples with the PI function

The number is used in calculating the area and volume of figures based on circles and spheres.

Area of a circle – Excel formula

The area of a circle A through radius r is calculated by the formula:

A = πr²

Let’s assume the radius is in cell A2, then the area formula will look like this:

=PI() * A2 ^ 2

Circumference – Excel formula

C = 2πr

If the circle radius is in cell A2, then the formula will be:

= 2 * PI() * A2

Area of a ring – Excel formula

A = π(R² - r²)

(where R is the outer radius and r is the inner radius). Let’s place the radii in cells A2 and B2, the formula:

= PI() * (A2 ^ 2 - B2 ^ 2)

Volume of a sphere – Excel formula

To calculate the volume of a sphere, only its radius is needed, and the geometric formula looks like this:

V = (4/3)πr³

Enter the required radius in cell A2 and use any other cell to calculate the volume of the sphere with the following Excel formula:

= 4 / 3 * PI() * A2 ^ 3

Surface area of a sphere – Excel formula

The mathematical formula for calculating the surface area of a sphere looks like this:

A = 4πr²

And the Excel formula will be like this (r in cell A2):

= 4 * PI() * A2 ^ 2

Volume of a cylinder – Excel formula

V = πr²h

Place the radius in cell A2 and the height in cell B2 and use the formula below:

= PI() * A2 ^ 2 * B2

Surface area of a cylinder – Excel formula

A = 2πrh + 2πr²

Here r is the radius, and h is the height of the cylinder. The corresponding cells: A2 and B2.

= 2 * PI() * A2 * B2 + 2 * PI() * A2 ^ 2

Volume of a cone – Excel formula

V = (1/3)πr²h

where r is the base radius, and h is the height of the cone.

In the formula below, these are A2 and B2 respectively:

= 1 / 3 * PI() * A2 ^ 2 * B2

Surface area of a cone – Excel formula

A = πr(l + r)

where r is the base radius, and l is the slant height of the cone. Let’s assume the radius is in cell A2, and the slant height of the cone is in cell B2. Then the formula will look like this:

= PI() * A2 * (A2 + B2)

Area of a circle inscribed in a triangle by the lengths of its three sides

Given a triangle and we know the lengths of all its sides. The triangle can be any shape. A circle is inscribed inside the triangle. We need to calculate the area of the circle outlined by it.

A complex but solvable geometric problem step by step. Below is its algorithm:

First, the semiperimeter of the triangle is calculated (sum of side lengths divided in half):

s = (a + b + c)/2

Then Heron’s formula is used to find the area A of the triangle through the semiperimeter and side lengths:

A = √(s(s-a)(s-b)(s-c))

The radius r of the inscribed circle equals the ratio of the triangle’s area to its semiperimeter:

r = A/s

Finally, knowing the radius of the circle, we use the circle area formula:

A = πr²

If we put all this together, the formula for the area of a circle inscribed in a triangle with sides of lengths a, b, and c looks as follows:

A = π((a + b + c)/2((a + b + c)/2-a)((a + b + c)/2-b)((a + b + c)/2-c))

Let’s imagine that the lengths of the triangle’s sides a, b, and c are in cells A2, B2, and C2 respectively:

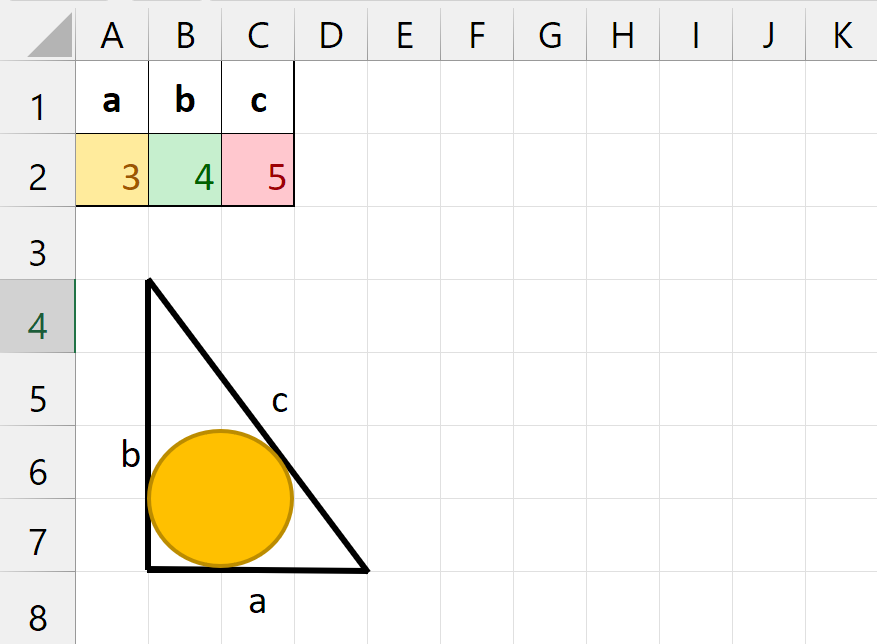
Then the final formula will be:

= PI() * (A2 + B2 + C2) / 2 * ((A2 + B2 + C2) / 2 - A2) * ((A2 + B2 + C2) / 2 - B2) * ((A2 + B2 + C2) / 2 - C2) / ((A2 + B2 + C2) / 2) ^ 2

This post is also available in RU.